Der Goldene Schnitt: berechnen und anwenden

Mit dem Goldenen Schnitt lassen sich Strecken und Flächen auf eine harmonische Art und Weise unterteilen. Wir begegnen dieser Streckenteilung viel häufiger, als wir denken – und wir zeigen, wie und wo Sie den Goldenen Schnitt ganz bewusst einsetzen können.

Von

Claudia

11. Juli 2023

Bei dem Goldenen Schnitt handelt es sich um ein Teilungsverhältnis von Strecken. Dieses Teilungsverhältnis wird als besonders harmonisch und anziehend empfunden und wurde bereits in der Antike von Künstlern und Bildhauern eingesetzt. Wer aufmerksam durch die Welt streift, findet diese „göttliche Proportion“ in der Natur und im menschlichen Körper, in der Architektur, in der Typografie und in der Gestaltung und sogar in der Musik. Für Gestalter stellt der Goldene Schnitt in mehrfacher Hinsicht eine gute Hilfe bei Strecken- und Raumaufteilungen dar.

Der Goldene Schnitt und seine Konstruktion

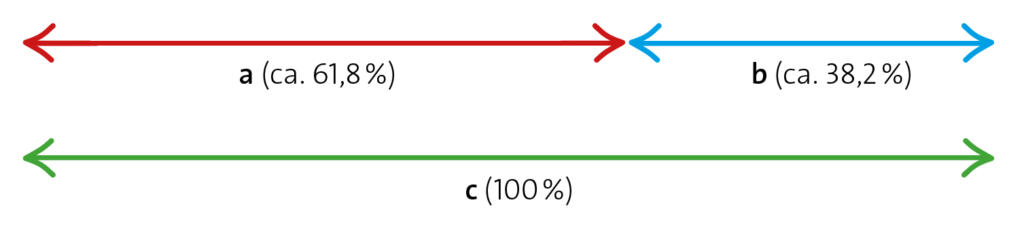
Die Konstruktion des Goldenen Schnitts lässt sich entweder einfach, aber auch sehr komplex erklären. Wir beginnen mit der einfachen Version: Man unterteilt eine Strecke so, dass sich das Verhältnis der kleinen Strecke zur größeren Strecke genauso verhält wie das Verhältnis von der größeren zur Gesamtstrecke. Die daraus resultierende Verhältniszahl lautet 1,61803398874… und wird Phi genannt, eine irrationale Zahl.

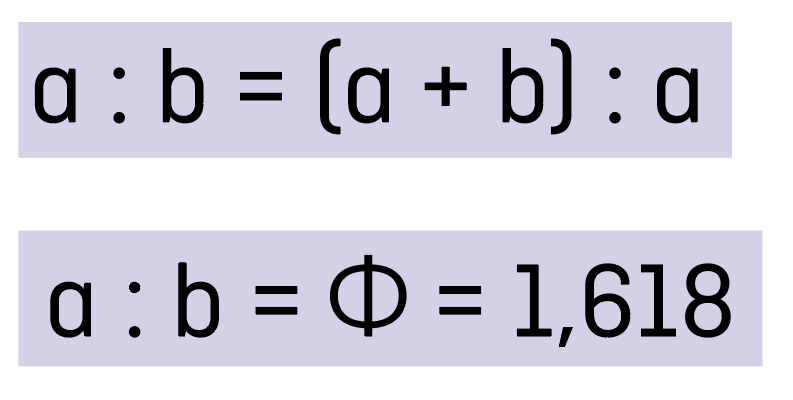
Mathematische Ausdrücke, die den Goldenen Schnitt darstellen. Der erste Ausdruck lautet a:b = (a+b):a, während der zweite den griechischen Buchstaben Phi zeigt, dargestellt als 1,618. Beide stehen auf einem hellgrauen Hintergrund. Ein Diagramm mit drei horizontalen Pfeilen veranschaulicht den Goldenen Schnitt. Der rote Pfeil mit der Aufschrift „a“ (ca. 61,8 %) und der blaue Pfeil mit der Aufschrift „b“ (ca. 38,2 %) bilden zusammen den grünen Pfeil mit der Aufschrift „c“ (100 %) und verkörpern so perfekt die Harmonie dieses Konzepts des Goldenen Schnitts.

Weitere Konstruktionsarten

Seit vielen Jahrhunderten wird mit dem Goldenen Schnitt gearbeitet, und so haben sich auch verschiedene Konstruktionsarten gebildet. Das klassischen Konstruktionsverfahren mit innerer Teilung ist eines der leicht zu verstehenden Vorgehensweisen, aber weitere Verfahren nach Euklid, nach Kurt Hofstetter oder nach Georg Odom sind ebenfalls bekannt. Beim klassischen Konstruktionsverfahren mit innerer Teilung wird wie folgt gearbeitet:

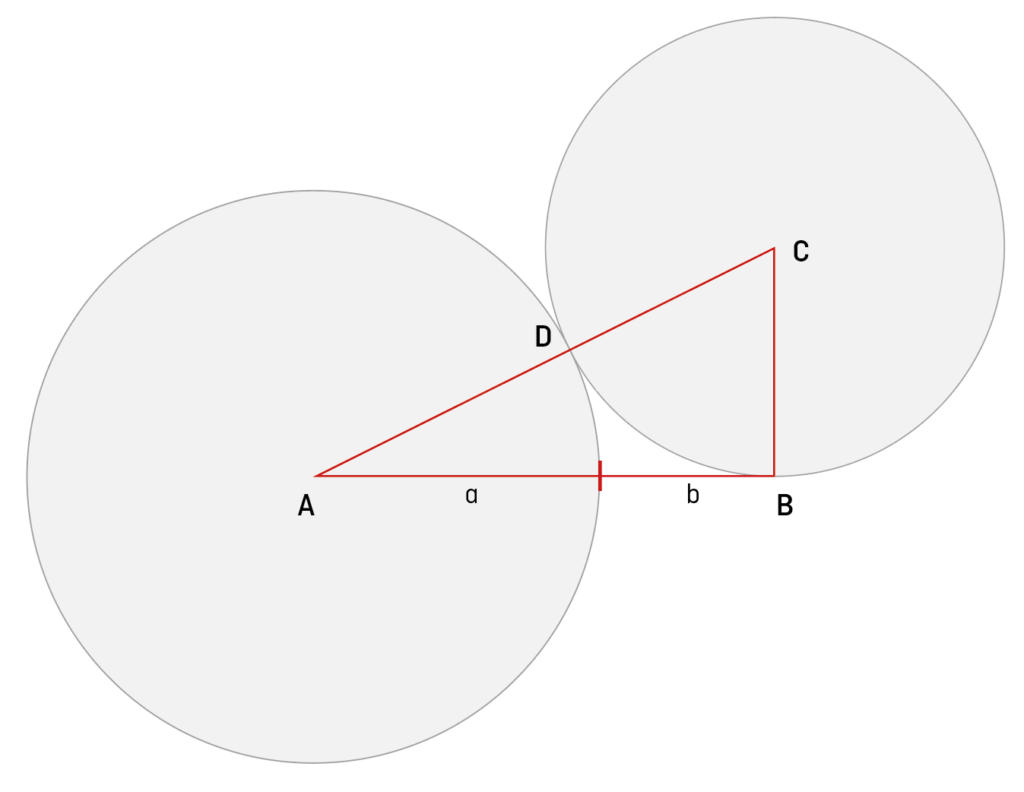
Wir zeichnen eine waagerechte Strecke von Punkt A bis Punkt B. Auf Punkt B startet eine Senkrechte, die halb so lang ist wie AB; das Ende dieser Strecke ist Punkt C. Wir zeichnen nun einen Kreis, der seinen Mittelpunkt bei C hat und einen Radius von BC aufweist. Dadurch entsteht auf der Strecke AC ein neuer Punkt namens D. Ein zweiter Kreis wird gezeichnet; sein Mittelpunkt ist A und sein Radius beträgt AD. Dieser Kreis schneidet unsere erste Waagerechte AB und unterteilt sie damit im Goldenen Schnitt.

Zwei sich überlappende Kreise mit beschrifteten Punkten: A auf dem linken Kreis, B auf dem rechten Kreis und ein rechter Winkel bei C. D ist der Schnittpunkt. Es werden die Liniensegmente AB, AC, BC und AD angezeigt; AB ist als „α“ und BC als „b“ gekennzeichnet. Die Komposition weist durch ihre harmonischen Proportionen auf den Goldenen Schnitt hin.

Rechenbeispiel

Sie möchten einmal proberechnen?

Ihre Gesamtstrecke beträgt 10 cm; eine Unterteilung in zwei Teilstrecken nach dem Goldenen Schnitt ergibt einen Wert von 6,18 cm für a und 3,82 für b.
(10 : 1,618 = 6,18)

Ihre längere Strecke a beträgt 15 cm und sie möchten b errechnen? b beträgt 9.27 cm, die Gesamtlänge beträgt 24,27 cm.
(15 : 1,618 = 9,27)

Ihre kürzer Strecke b beträgt 8 cm und Sie möchten a errechnen? a weist eine Länge von 12,94 cm auf.
(8 x 1,618 = 12,94)

Wer lieber rechnen lassen möchte, kann diesen Rechner verwenden: https://jumk.de/goldener-schnitt/

Goldene Geometrie: Rechteck, Dreieck, Winkel und Spirale

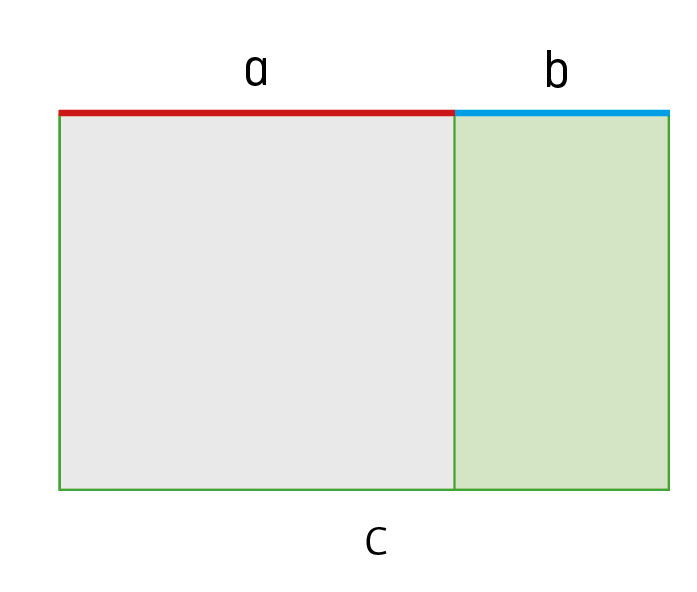
Auch das gibt es: ein Goldenes Rechteck. Dabei handelt es sich um ein Rechteck, dessen Seitenverhältnisse dem Goldenen Schnitt entsprechen. Beim Goldenen Dreieck handelt es sich um ein gleichschenkliges Dreieck, bei dem die beiden gleichschenkligen Seiten das Streckenverhältnis des Goldenen Schnitts aufweisen. Für den Goldenen Winkel teilt man die 360 Grad eines Kreises gemäß des Goldenen Schnitts. Und bei der Goldenen Spirale handelt es sich um eine Spirale, deren Wachstum sich am Goldenen Schnitts orientiert. Genauer gesagt wächst sie pro Viertelumdrehung um den Faktor Phi und erinnert uns an die Nautilusmuschel.

das Goldene Rechteck

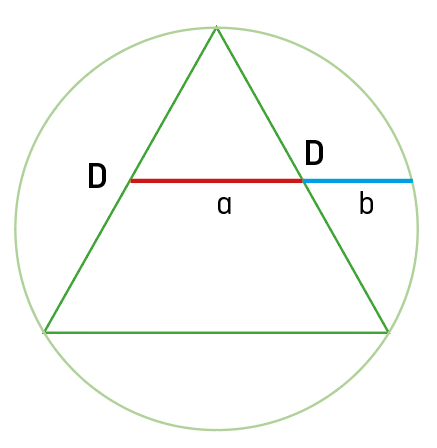
Der Goldene Schnitt wird durch ein Rechteck verkörpert, das in Abschnitte unterteilt ist: die breitere linke Seite, „a“, ist oben mit einer roten Linie versehen, und die schmalere rechte Seite, „b“, ist blau hervorgehoben. Die Basis ist mit „c“ gekennzeichnet und durch eine grüne Umrandung hervorgehoben, wodurch die Proportionen harmonisch ausgeglichen werden.

das Goldene Dreieck

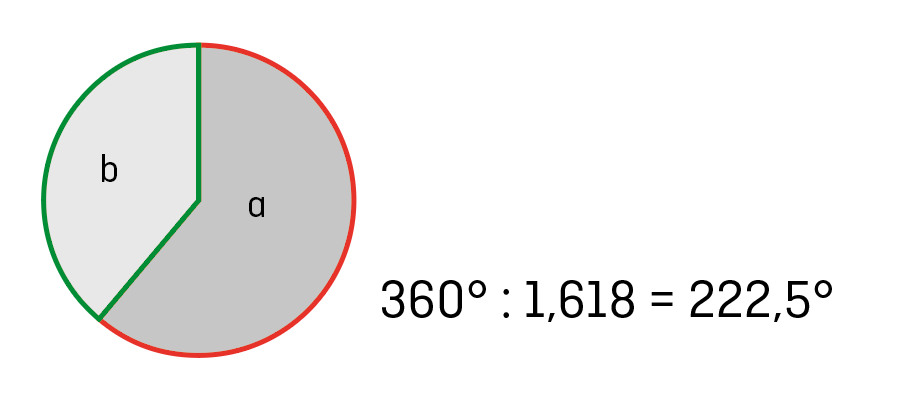
Ein grünes Dreieck, das in einen Kreis eingeschrieben ist, weist innen eine rote Linie mit der Bezeichnung „a“ und außen eine blaue Linie mit der Bezeichnung „b“ auf, die eine Seite leicht berührt. Die Hypothenuse des Dreiecks mit der Bezeichnung „D“ spiegelt in ihren harmonischen Proportionen den Goldenen Schnitt wider.

der Goldene Kreis

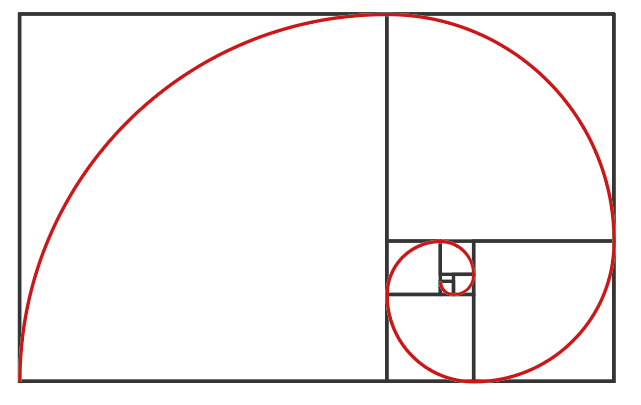
Ein Kreis, der in zwei Sektoren unterteilt ist, „a“ und „b“, wobei „a“ größer ist. Der Rand von „a“ ist rot, während „b“ grün ist. Neben dem Kreis illustriert die Gleichung „360° ÷ 1,618 = 222,5°“, die den Goldenen Schnitt darstellt, auf elegante Weise den Goldenen Schnitt in der Geometrie.

die Goldene Spirale

Eine Fibonacci-Spirale mit grünem Farbverlauf, die „Der Goldene Schnitt“ verkörpert, weist Rechtecke mit den Bezeichnungen 13, 8, 5 und 2 auf. Die Größe jedes Rechtecks entspricht der Fibonacci-Folge, wobei dunklere Grüntöne die kleineren Bereiche hervorheben. Ein schwarz umrandetes Rechteck ist in Quadrate mit einer roten Spirale unterteilt und illustriert den Goldenen Schnitt. Die Spirale beginnt klein im innersten Quadrat und dehnt sich elegant durch die größeren Abschnitte aus.

Der Goldenen Schnitt und seine Geschichte

Eine erste überlieferte Beschreibung des Goldenen Schnittes (noch unter anderem Namen) stammt vom griechischen Mathematiker Euklid, der ca. 300 v Chr. lebte. Allerdings geht man davon aus, dass das Teilungsverhältnis bereits zuvor auch in anderen Gebieten wie China angewendet wurde. Speziell in der Renaissance mit ihrer Wiederbelebung der Kultur aus der griechischen und römischen Antike stellte man den Goldenen Schnitt auch in einen philosophischen Zusammenhang. Man findet ihn in Schriften von Mathematiker Luca Pacioli sowie in Werken von Künstler wie Leonardo da Vinci und Albrecht Dürer.

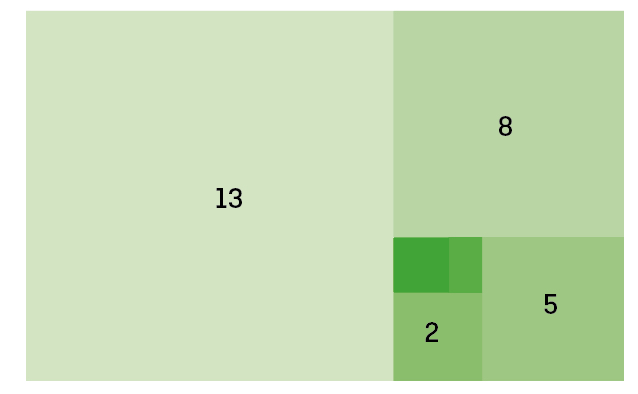
Der Goldene Schnitt und die Fibonacci-Folge

Mit der Fibonacci-Folge hat der Mathematiker Leonardo von Pisa, auch Fibonacci genannt, Anfang des 13. Jahrhunderts eine Zahlenreihe entwickelt, die den Zahlen des Goldenen Schnitts ähnelt. Bei dieser Zahlenreihe, die basierend auf der Populatoin von Kaninchen entstand, ist die nächste Zahl die Summe der zwei vorhergehenden Zahlen.

1+0=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13

Folge: 2 : 3 : 5 : 8 : 13 : 21 : 34 : 55 : 89 : 144 : 233 …

Gehen Sie auf die Suche!

Blätter, Blüten, Käfer, Tannenzapfen – in der Natur finden Sie unzählige Beispiele für die Schönheit und Harmonie der ästhetischen Raumaufteilung. Der Goldene Schnitt findet sich zum Beispiel in Blättern von Blumen und Pflanzen.

Nahaufnahme einer großen grünen Sukkulente mit symmetrischen, überlappenden Blättern, die spiralförmig angeordnet sind und die Prinzipien des Goldenen Schnitts verkörpern. Das Sonnenlicht erzeugt Schatten und hebt die glänzende Textur der Blätter hervor.

Goldener_Schnitt_Bild_4

Wenn Sie architektonisch stöbern möchten, dann betrachten Sie die Cheops-Pyramide bei Gizeh, der Tempel Panthenon auf der Akropolis, das Taj Mahal in Indien, den Königsplatz in München, die Frankfurter Paulskirche, die Berliner Nationalgalerie, das Alte Museum auf der Museumsinsel, das Konzerthaus, den deutschen oder den französischen Dom. Auch wenn gerade bei antiken Bauten häufig der Nachweis fehlt, dass die Proportionen des Goldenen Schnitts bewusst oder intuitiv angewendet wurden – die harmonische Wirkung ist nicht zu übersehen.

Das Taj Mahal, ein Mausoleum aus weißem Marmor, das für den Goldenen Schnitt bekannt ist, verfügt über eine große zentrale Kuppel und symmetrische Minarette an jeder Ecke. Ein langer reflektierender Pool führt Sie zum Eingang, umgeben von gepflegten Gärten unter klarem Himmel.

Auch in der Fotografie ist der Goldene Schnitt ein Begriff und kann bei der Bildaufteilung beziehungsweise bei der Platzierung von Motiven unterstützen. Meist wird hier jedoch großzügig gerundet und mit der Drittelregel gearbeitet.

Berechenbare Schönheit

Aber nicht nur in der Kunst, in der Architektur oder in der Natur sucht man danach. Laut dem „Goldenen Schnitt der Schönheit“ lassen sich auch Gesichter nach dem Verhältnis von 1:1,61 scannen und bewerten; je näher die Ergebnisse der Streckenteilungen an 1,61 liegen, umso „schöner“ soll das Gesicht empfunden werden.

Goldener Schnitt in Gestaltung und Layout

Das Papierformat basiert üblicherweise auf den DIN-Formaten, was wiederum Preisvorteile im Druck hat. Wer davon abweichen möchte, kann auch ein Papierformat basierend auf dem Goldenen Schnitt bzw. der Fibonacci-Reihe verwenden. Auch bei der Satzspiegelfindung gibt es verschiedene Konstruktionen: die Linienkonstruktion, die Neuerteilung und eben auch die Satzspiegelberechnung nach dem Goldenen Schnitt, über die Sie im Artikel Satzspiegel-Crashkurs: So gestalten Sie harmonische Layouts mehr erfahren können.

Wer für die Raumaufteilung mit einem Gestaltungsraster als Ordnungssystem arbeitet, kann ebenfalls auf die Harmonie der Proportionen zurückgreifen und anhand dessen Flächen oder Objekte platzieren. Im besten Fall basieren dann Papiergröße, Satzspiegel und Gestaltungsraster gemeinsam auf den ausgewogenen Maße.

Logo-Design im Goldenen Schnitt

Der Goldene Schnitt dient häufig auch als Basis im Logo-Design. Wer genauer hinsieht, wird das eine oder andere Logo entdecken, dass auf einem Wert von 1:1,61 basiert wie zum Beispiel das von Twitter, von Apple oder von icloud.

Die Maße der Schönwetter-Wolke von icloud basieren – leicht gerundet – auf drei verschieden großen Kreisen, deren Größenverhältnis 1:1,618 beträgt. Genau genommen handelt es sich um zwei Kreispaare im ästhetischen Teilungsverhältnis. Auch weisen die Außenmaße des Logos (Breite zu Höhe) ein Verhältnis im Goldenen Schnitt auf.

Das icloud-Logo
Der Goldene Schnitt ist auch im icloud-Logo zu finden. Die Wolkenform basiert auf zwei Kreispaaren, deren Größenverhältnisse entsprechend gewählt sind (Mitte). Die Seitenverhältnisse von Breite und Höhe stehen ebenfalls im Verhältnis von 1:1,618.

Symbol einer weißen Wolke auf einem blauen Hintergrund mit Farbverlauf, das einen Cloud-Speicher mit harmonischen Proportionen darstellt, die an „Der Goldene Schnitt“ erinnern. App-Symbol mit einer Wolkenform aus überlappenden roten und blauen Kreisen auf einem blauen Hintergrund mit Farbverlauf. Die weiß umrandete Wolke spiegelt auf subtile Weise die Harmonie des Goldenen Schnitts wider. Ein blaues quadratisches Symbol mit einer stilisierten weißen Wolke in der Mitte, die auf elegante Weise den Goldenen Schnitt enthält. Die Wolke ist mit einer harmonischen Anordnung geometrischer Formen, darunter Kreise und Rechtecke, überlagert, die ihre Komposition umreißen.

Auch wenn wissenschaftliche Belege fehlen und immer wieder zu lesen ist, dass der Goldenen Schnitt und sein ästhetischer Wert überschätzt wird, arbeiten wir Gestalter trotzdem häufig intuitiv mit diesen Proportionen – und empfinden sie als schön.

Bildquellen: Piotr Wytrazek, Kiev.Victor, Tramont_ana via Shutterstock.com; WikiImages; yosratawakol, MoneyforCoffee via Pixabay.com